So modellierst Du lineare Funktionsgleichungen!

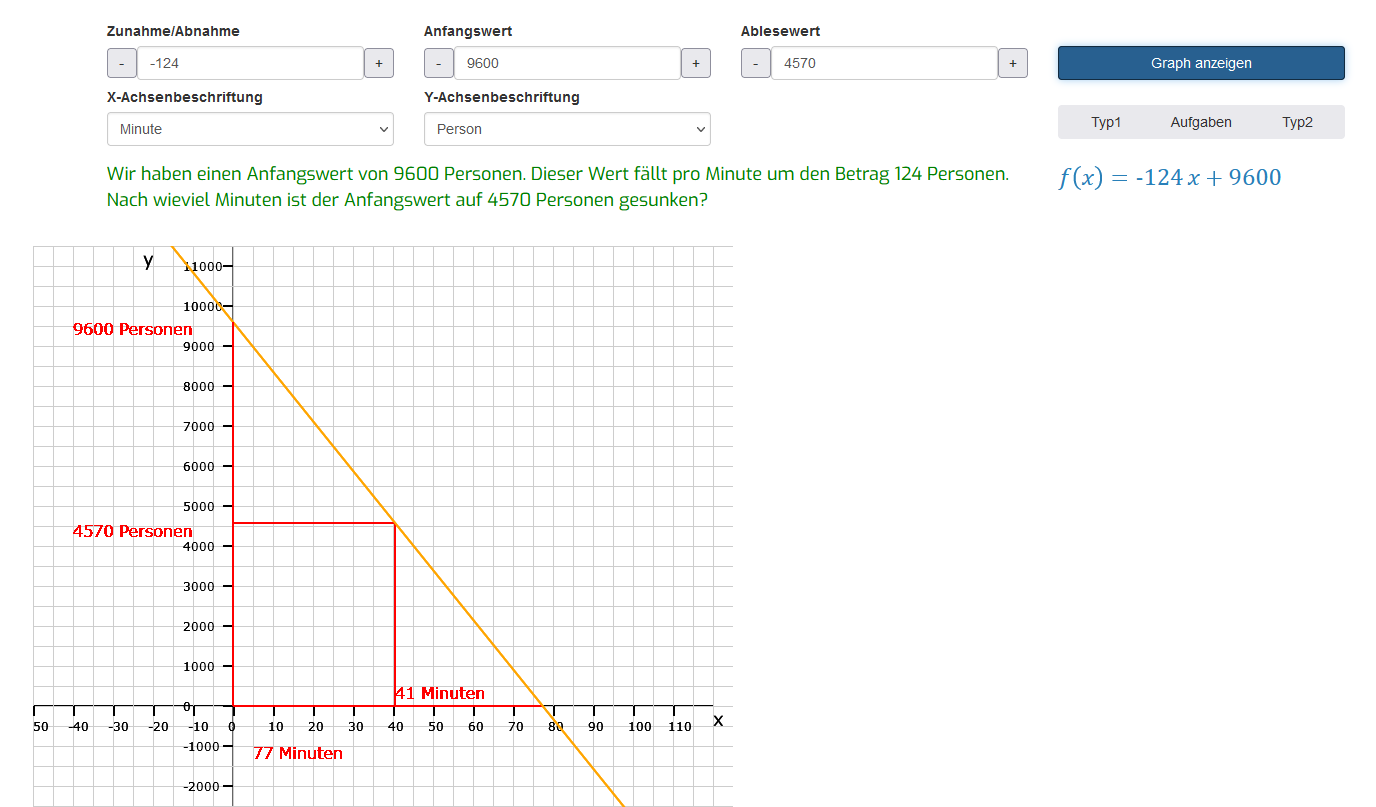
Es gibt zwei Typen von Modellierungsaufgaben. Im ersten Typ wird ein Anfangswert, wie zum Beispiel ein bestimmter €-Betrag bei einer Taxifahrt, genannt und, um bei diesem Beispiel zu bleiben, ein Betrag, der bei jedem Kilometer zum Anfangsbetrag addiert wird. Hier gibt es grundsätzlich zwei Aufgabenstellungen: Erstelle aufgrund der Angaben die Funktionsgleichung und wie hoch ist der Gesamtbetrag nach einer bestimmten Zeiteinheit oder Distanz. Beim zweiten Typ geht es um die stetige Abnahme eines Anfangswerts, also nicht um einen steigenden, sondern um einen fallenden Graphen. Neben der Erstellung der entsprechenden Funktionsgleichung, gibt es hier in der Regel zwei Fragestellungen: Nach welcher zeitlichen oder räumlichen Einheit sinkt der Anfangswert auf 0? Auf welchen Wert sinkt der Anfangswert nach einer bestimmten Zeit oder räumlichen Distanz?

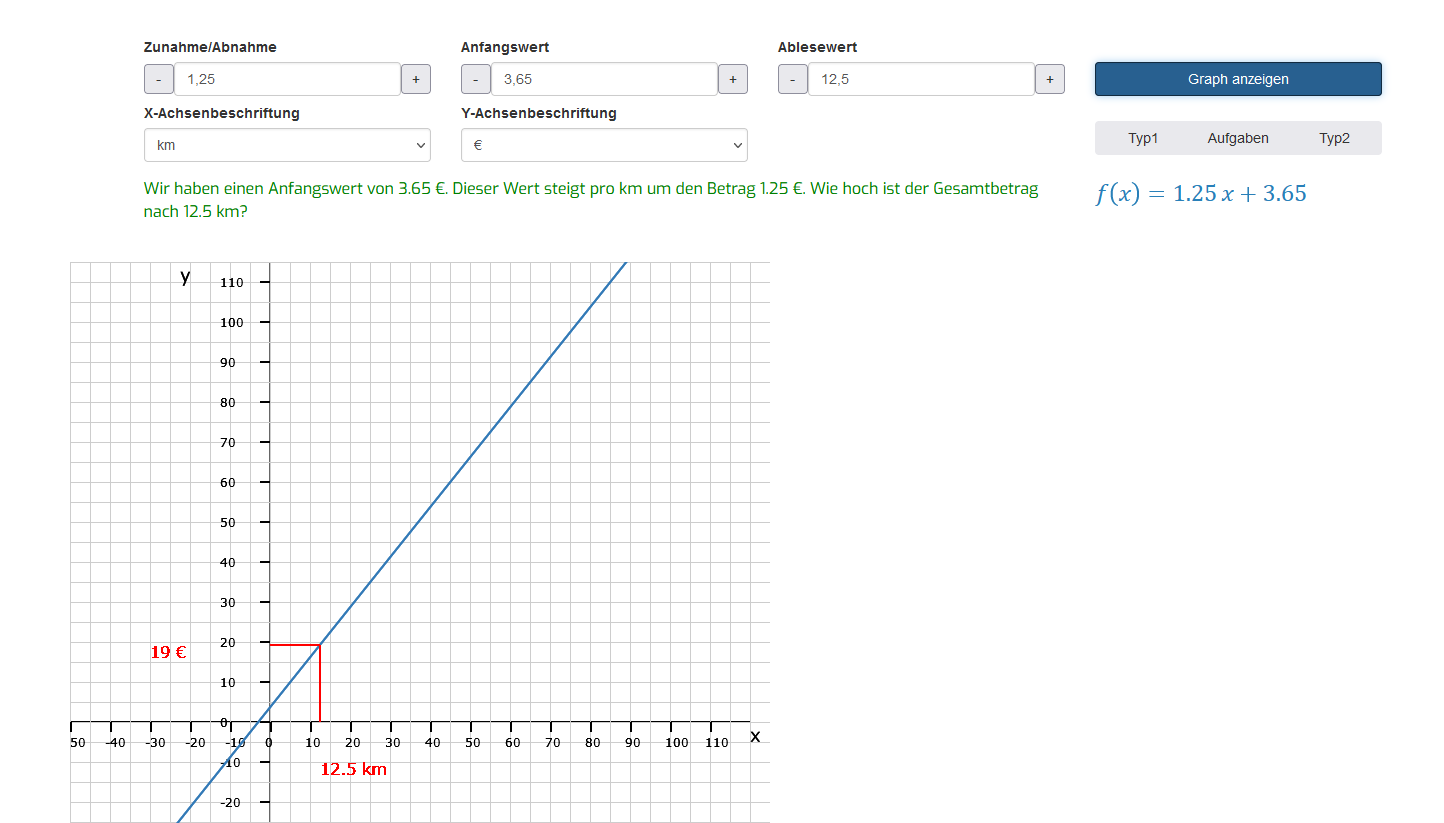
Hier siehst Du Eingabefelder, in die die Angaben einer typischen Anwendungsaufgabe eingetragen wurden. Die Aufgabe lautet: Ein Taxiunternehmen nimmt pro Fahrt eine Grundgebühr von 3,65 €. Pro Kilometer erhöht sich der Gesamtbetrag um 1,25 €. Wie hoch ist die Taxirechnung nach 12,5 gefahrenen Kilometern?

Diese Art von Aufgabe nennen wir hier Typ1-Aufgabe. Es gibt einen niedrigen Anfangswert, auch y-Achsenabschnitt genannt, wo die Gerade die y-Achse schneidet. Den Schnittpunkt erhalten wir gemäß der allgemeinen Geradengleichung y = m · x + b, wenn wir x = 0 setzen, worauf das Produkt von m · x zu Null wird. Hat dann b einen positven oder negativen Wert, so ist das der Wert für y. In unserem Beispiel 3,65 €. Der Betrag, der pro gefahrenem Kilometer zum Anfangsbetrag addiert wird, entspricht unserem Steigungsfaktor m, in diesem Fall 1,25 €. Da pro Kilometer der Gesamtbetrag somit steigt, ist m > 0 und die Gerade steigt. Der Gesamtbetrag nach 12,5 gefahrenen Kilometern beträgt 19 € und lässt sich in der Graphik ablesen. Berechnen lässt sich das, wenn man die von der App ermittelten Funktionsgleichung die 12,5 für x einsetzt und die Gleichung nach y auflöst.

Im zweiten Bild geht es um eine Aufgabe vom Typ2. Hier nimmt ein relativ hoher Anfangswert stetig ab. Diese Beispielaufgabe könnte lauten: In einem Stadion befinden sich 9600 Zuschauer. Nach Spielende verlassen pro Minute 124 Personen das Stadion durch 2 Ausgänge. Wie lange dauert es, bis die Zahl der noch verbliebenen Zuschauer auf 4570 Personen gesunken ist?

Wieder tragen wir die Angaben in der Aufgabe in die richtigen Felder ein. Da es sich um eine Abnahme handelt, ist es wichtig, als Abnahmefaktor eine negative Zahl einzutragen. Gemäß der gestellten Aufgabe tragen wir die Zahl der noch verbliebenen Zuschauer in das Feld "Ablesewert" ein. Lassen wir dieses Feld leer, wird lediglich angezeigt, nach wieviel Minuten das Stadion leer ist.

Auch hier wird eine Funktionsgleichung gemäß Deiner Einträge angezeigt. Wechselst Du den Aufgabentyp, wird wieder der Graph in seiner Ausgangsposition angezeigt: f(x) = x. Der Aufgabentext ist in einer Allgemeinform gehalten. Erst durch Zugabe der Werte und Einheiten aus einer Aufgabe Deiner Wahl, ändert sich der Aufgabentext. Du kannst jetzt auch andere, beliebige Werte eintragen und sehen, wie sich die Ausrichtung der Geraden und die Skalierungen von x-Achse und y-Achse verändern. Hier Erfahrungen zu sammeln ist wichtig, wenn die Aufgabe lautet: Zeichne die Gerade in ein Koordinatensystem mit einer der Aufgabe angepassten Skalierung.